3D模型平面切割

muzzik大约 9 分钟

# 前言

一年一度的征稿到了，倒腾点存货，3D平面切割通常用于一些解压游戏里，例如水果忍者，切菜这些，今天我就给大家讲讲怎么实现3D切割以及其原理，帮助大家更理解3D中的 Mesh(网格)，以及UV贴图和法线

由于和参赛帖另一篇文章主题相同，先自证一下这是存货
本来想等 Store 审核通过再发，但是免得大家说我抄袭就先上了

# 准备工作

了解模型

想要切割一个模型，首先要了解模型是怎么组成的，其实所有模型都是由一个个三角面组成，如下

一个平面最少由两个三角形组成，而模型就是由多个三角形组成，我们要切割模型，其实就是做三角形的分割
做三角形的分割，首先我们需要一个方向，在 2D 中是一个方向向量，在 3D 中就是一个平面

创建平面对象

在 Creator3.x 版本下怎么创建这个平面对象？在 cc.geometry 中有很多几何对象类型，我们就使用其中的 cc.geometry.Plane 进行创建

const node_ui_transform =
	node_.getComponent(cc.UITransform) ||
	node_.addComponent(cc.UITransform);
const panel_ui_transform =
	panel_.getComponent(cc.UITransform) ||
	panel_.addComponent(cc.UITransform);

this._plane = cc.geometry.Plane.fromNormalAndPoint(
	new cc.geometry.Plane(),
	// 法线方向（基于被切割节点坐标系，平面上方到自身的方向向量）
	node_ui_transform
		.convertToNodeSpaceAR(
			panel_ui_transform.convertToWorldSpaceAR(cc.Vec3.UP)
		)
		.subtract(
			node_ui_transform.convertToNodeSpaceAR(panel_.worldPosition)
		)
		.normalize(),
	// 平面在切割节点的本地坐标
	node_ui_transform.convertToNodeSpaceAR(panel_.worldPosition)
);

node_：被切割节点
panel_：平面节点

获取网格数据

有了用于切割时的平面对象，我们还需要 Mesh 数据，这些数据有什么？看下图

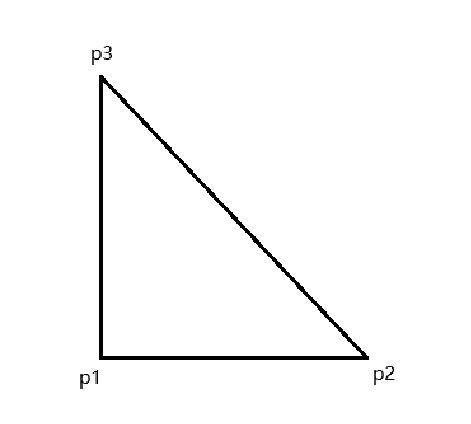
顶点数据：例如 [p1,p2,p3]，存放所有三角形点的坐标数据
顶点索引：例如 [0,1,2]，是顶点数据数组的下标，用来指定下标的数据组成一个三角形

怎么获取？

// 获取 cc.Mesh
this._mesh = node_.getComponent(cc.MeshRenderer)!.mesh!;

/** 网格数据 */
const mesh = cc.utils.readMesh(this._mesh, 0);

注意，这里只是获取的下标为 0 的子网格，如果一个模型包含多个子网格，那么还是需要遍历获取再切割，可以通过 this._mesh.struct.primitives.length 获取子网格数量

# 开始切割

前面说了模型是由一个个三角形组成的，那么我们只需要遍历模型的网格数据针对每个和平面相交的三角形切割就行了

首先需要准备两个 cc.primitives.IGeometry 类型的对象，用于分别存储正反面的网格数据
遍历需要切割的网格三角形数据，与平面相交就切割三角形后放入对应的 cc.primitives.IGeometry，不相交就不需要切割

/** 三角形点 */
const triangle_point_as = [
	new _mesh_slicer.point_data(),
	new _mesh_slicer.point_data(),
	new _mesh_slicer.point_data(),
];
/** 正面 */
const positive_geometry = (this._positive_mesh.geometry =
	this._create_geometry());
/** 反面 */
const negative_geometry = (this._negative_mesh.geometry =
	this._create_geometry());

// 遍历三角形切割
for (
	let k_n = 0, len_n = geometry_.indices!.length;
	k_n < len_n;
	k_n += 3
) {
	/** 三角形索引 */
	const indices_ns = [
		geometry_.indices![k_n],
		geometry_.indices![k_n + 1],
		geometry_.indices![k_n + 2],
	];

	...
}

判断三角形是否与平面相交

这里我们只需要知道三角形的顶点是否在平面的正面或者反面就可以判断是否相交，
如果三个点全在一侧则肯定不相交，如果不全在一侧则一点相交 ，我们可以使用点乘 dot 判断在平面的哪一侧

// 平面的法线 dot(三角形点)  - 平面距离原点距离 > 0 即为正面
positive_b = this._plane.n.dot(p) - this._plane.d > 0;

和上面说的一样，如果三角形的三个点 positive_b 一致则是全在平面的一侧不需要切割，不一致则需要切割

// 所有顶点都在同一侧
if (
	triangle_point_as[0].positive_b === triangle_point_as[1].positive_b &&
	triangle_point_as[1].positive_b === triangle_point_as[2].positive_b
) {
	const mesh = triangle_point_as[0].positive_b
		? this._positive_mesh
		: this._negative_mesh;

	// 更新旧索引
	triangle_point_as.forEach((v) => {
		this._update_old_indices(mesh, v);
	});

	// 添加点到几何数据
	this._add_point_to_geometry(mesh.geometry, triangle_point_as);
}
// 不在同一侧则切割三角形
else {
	// 顶点 0,1 在同一侧
	if (
		triangle_point_as[0].positive_b === triangle_point_as[1].positive_b
	) {
		this._slice_triangle([
			triangle_point_as[2],
			triangle_point_as[0],
			triangle_point_as[1],
		]);
	}
	// 顶点 0,2 在同一侧
	else if (
		triangle_point_as[0].positive_b === triangle_point_as[2].positive_b
	) {
		this._slice_triangle([
			triangle_point_as[1],
			triangle_point_as[2],
			triangle_point_as[0],
		]);
	}
	// 顶点 1,2 在同一侧
	else {
		this._slice_triangle([
			triangle_point_as[0],
			triangle_point_as[1],
			triangle_point_as[2],
		]);
	}
}

切割三角形

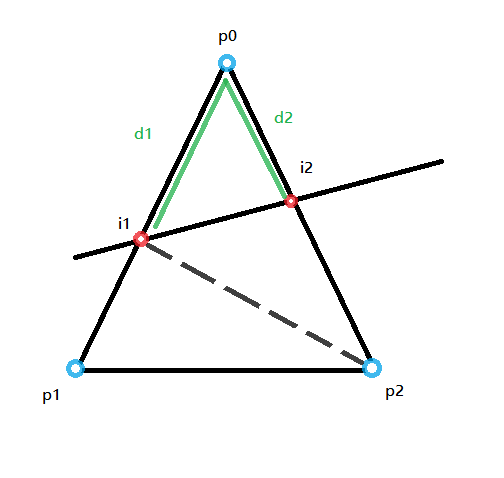
(i1, i2) ：平面
(p0, p1, p2) ：原本的三角形（逆时针为正面）
(p0, i1, i2) ：切割后的三角形
(i1, p1, p2) : 切割后的三角形2
(i2, i1, p2) : 切割后的三角形3

如果三角形三个顶点形成的线段不与平面相交，那么则不需要新建顶点
如果三角形线段与平面相交，则切割为三个三角形，怎么判断相交，看下面

怎么确定交点（i1, i2）？

交点也就是 i1，i2 的坐标，知道了交点才能分割三角形，以下以获取 i1 的坐标为例

射线公式：P = P0 + tV；
平面公式：A(P−P1) = 0；

这两个公式里， P 是射线上也在平面上的一个点，也就是射线和平面的交点。 P0 是射线的起点， V 是射线的方向。 t 是一个数字，当它变化时，P就会在射线上移动。 P1 是平面上的一个特定点， A 是平面的法向量。

我们将射线的公式代入到平面的公式中，就得到： A(P0 + tV - P1) = 0，求解为：t = (A * (P1 - P0))/(A * V)，这里 Creator 有内置的函数，就不用自己写了

步骤为：

确定 i1 的坐标，从 p0 到 p1 的方向创建一条射线
```
cc.geometry.Ray.fromPoints(ray, p0, p1);
```

计算与平面的交点距离

const distance_n = cc.geometry.intersect.rayPlane(ray, this._plane);

获取交点坐标
```
ray.computeHit(point, distance_n);
```

这样就得到了交点，除了交点，我们还要计算法线和UV

法线和UV

法线

法线就是决定你模型的凹凸效果的，它存在于每个顶点数据中，是一个三维向量

UV

UV 就是你的模型贴图的图片坐标，它决定了你这个顶点位置展示的贴图内容在图片的什么部分，是一个二维向量

法线和UV的计算很简单，根据交点的位置使用 lerp 函数从起点和终点线段做一个插值就行了

/**
 * 获取线段和平面交点
 * @param point_as_ 线段起始和结束点
 * @param out_point_ 输出点
 * @returns
 */
private _get_line_segment_and_plane_intersect(
	out_point_: _mesh_slicer.point_data,
	point_as_: _mesh_slicer.point_data[]
): _mesh_slicer.point_data {
	/** 射线 */
	const ray = cc.geometry.Ray.fromPoints(this._temp_tab.ray, point_as_[0].position_v3, point_as_[1].position_v3);
	/** 距离 */
	const distance_n = cc.geometry.intersect.rayPlane(ray, this._plane);
	/** 两点之间的长度 */
	const line_length_n = this._temp_tab.value_v3.set(point_as_[0].position_v3).subtract(point_as_[1].position_v3).length();

	// 计算碰撞位置
	ray.computeHit(out_point_.position_v3, distance_n);
	// 计算 uv
	cc.Vec2.lerp(out_point_.uv_v2, point_as_[0].uv_v2, point_as_[1].uv_v2, distance_n / line_length_n);
	// 计算法线
	cc.Vec3.lerp(out_point_.normal_v3, point_as_[0].normal_v3, point_as_[1].normal_v3, distance_n / line_length_n);

	return out_point_;
}

/**
		 * 获取线段和平面交点
		 * @param point_as_ 线段起始和结束点
		 * @param out_point_ 输出点
		 * @returns
		 */
		private _get_line_segment_and_plane_intersect(
			out_point_: _mesh_slicer.point_data,
			point_as_: _mesh_slicer.point_data[]
		): _mesh_slicer.point_data {
			/** 射线 */
			const ray = cc.geometry.Ray.fromPoints(this._temp_tab.ray, point_as_[0].position_v3, point_as_[1].position_v3);
			/** 距离 */
			const distance_n = cc.geometry.intersect.rayPlane(ray, this._plane);
			/** 两点之间的长度 */
			const line_length_n = this._temp_tab.value_v3.set(point_as_[0].position_v3).subtract(point_as_[1].position_v3).length();

			// 计算碰撞位置
			ray.computeHit(out_point_.position_v3, distance_n);
			// 计算 uv
			cc.Vec2.lerp(out_point_.uv_v2, point_as_[0].uv_v2, point_as_[1].uv_v2, distance_n / line_length_n);
			// 计算法线
			cc.Vec3.lerp(out_point_.normal_v3, point_as_[0].normal_v3, point_as_[1].normal_v3, distance_n / line_length_n);

			return out_point_;
		}
/**
 * 切割三角形
 * @param point_as_ 三角形点（逆时针，首个点切割后为单三角）
 */
private _slice_triangle(point_as_: _mesh_slicer.point_data[]): void {
	/** 单三角网格 */
	const mesh = point_as_[0].positive_b
		? this._positive_mesh
		: this._negative_mesh;
	/** 双三角网格 */
	const mesh2 = point_as_[0].positive_b
		? this._negative_mesh
		: this._positive_mesh;

	// 获取交点
	this._get_line_segment_and_plane_intersect(this._temp_tab.point, [
		point_as_[0],
		point_as_[1],
	]);
	this._get_line_segment_and_plane_intersect(this._temp_tab.point2, [
		point_as_[0],
		point_as_[2],
	]);

	// 添加单三角
	{
		// 更新索引
		this._update_new_indices(mesh, this._temp_tab.point, point_as_[1]);
		this._update_new_indices(mesh, this._temp_tab.point2, point_as_[2]);
		this._update_old_indices(mesh, point_as_[0]);

		// 添加三角
		this._add_point_to_geometry(mesh.geometry, [
			point_as_[0],
			this._temp_tab.point,
			this._temp_tab.point2,
		]);
	}

	// 添加双三角
	{
		// 更新索引
		this._update_new_indices(mesh2, this._temp_tab.point, point_as_[1]);
		this._update_new_indices(mesh2, this._temp_tab.point2, point_as_[2]);
		this._update_old_indices(mesh2, point_as_[1]);
		this._update_old_indices(mesh2, point_as_[2]);

		// 添加三角
		this._add_point_to_geometry(mesh2.geometry, [
			this._temp_tab.point2,
			this._temp_tab.point,
			point_as_[1],
		]);
		this._add_point_to_geometry(mesh2.geometry, [
			this._temp_tab.point2,
			point_as_[1],
			point_as_[2],
		]);
	}
}

简单来说就是根据交点将原本的 1 个三角形分为 3 个三角形，再根据自己正反面的位置添加到对应的正反面网格数据中并更新索引

# 生成平面

在切割结束后如果没有问题你会发现这是个空心模型，如果我们需要一个平面封住切口呢？怎么做？
这就被称为平面的 三角剖分

简单的三角剖分方案

求平均点，不完全支持凹多边形
左右横跳，不完全支持凹多边形
单点遍历，不完全支持凹多边形

不支持凹面多边形的后果

可以看下图

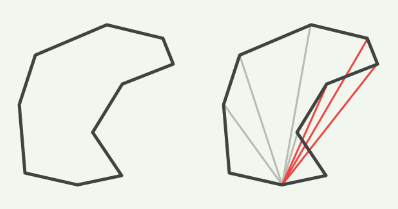
这样的话，无论是使用平均点，还是图中的单点遍历新建三角形，都会有可能出现生成的三角形错误的情况

那么如何做？步骤如下

记录新增的顶点坐标并排序（连线）
将排序后的多边形顶点分解为凸多边形
为所有凸多边形生成三角形

怎么判断凹凸？

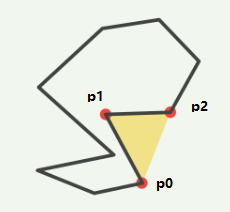
判断 p0 - p1 - p2 的夹角角度即可，这也是我们需要对新增顶点坐标排序的原因

将凹多边形分解为凸多边形

在找到凹角之后，我们只需要从 p1 的位置开始遍历至顶点，只要找到 p0 - p1 - pn 夹角不为凹角的 pn 顶点就可以分割为两个多边形，再对分割后的多边形重复执行此操作

平面带孔的情况

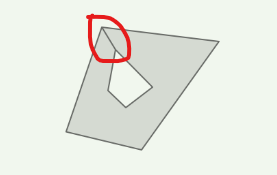
将排序后的两个多边形合并为一个，将内多边形的点连接到最近的一个外多边形，组合成为一个单独的多边形

但是还有一个问题，那就是单独的两个多边形可以依靠法线和碰撞检测来判断当前多边形是否在另一个内，那么多个多边形嵌套呢？

我这里想到的是使用面积判断，从大到小对多边形排序，内多边形的面积一定比外多边形小

# 源码

保证切割后模型原表面法线、UV 的正常
切口平面支持凹多边形
支持同时切割多个模型
使用共享顶点，可以节省模型内存占用

3D模型平面切割

# 前言

# 准备工作

了解模型

创建平面对象

获取网格数据

怎么获取？

# 开始切割

判断三角形是否与平面相交

切割三角形

怎么确定交点（i1, i2）？

法线和UV

法线

UV

# 生成平面

简单的三角剖分方案

不支持凹面多边形的后果

那么如何做？步骤如下

怎么判断凹凸？

将凹多边形分解为凸多边形

平面带孔的情况

# 源码

Cocos Store：https://store.cocos.com/app/detail/6118open in new window

# 其他参赛文章

原生预览调试！我给Cocos加了个新功能，原生开发者福音open in new window

📣 觉得很赞？分享给你的朋友吧！

3D模型平面切割

# # 前言

# # 准备工作

# 了解模型

# 创建平面对象

# 获取网格数据

# 怎么获取？

# # 开始切割

# 判断三角形是否与平面相交

# 切割三角形

# 怎么确定交点（i1, i2）？

# 法线和UV

# 法线

# UV

# # 生成平面

# 简单的三角剖分方案

# 不支持凹面多边形的后果

# 那么如何做？步骤如下

# 怎么判断凹凸？

# 将凹多边形分解为凸多边形

# 平面带孔的情况

# # 源码

# Cocos Store：https://store.cocos.com/app/detail/6118open in new window

# # 其他参赛文章

# 原生预览调试！我给Cocos加了个新功能，原生开发者福音open in new window

📣 觉得很赞？分享给你的朋友吧！

# 前言

# 准备工作

了解模型

创建平面对象

获取网格数据

怎么获取？

# 开始切割

判断三角形是否与平面相交

切割三角形

怎么确定交点（i1, i2）？

法线和UV

法线

UV

# 生成平面

简单的三角剖分方案

不支持凹面多边形的后果

那么如何做？步骤如下

怎么判断凹凸？

将凹多边形分解为凸多边形

平面带孔的情况

# 源码

Cocos Store：https://store.cocos.com/app/detail/6118open in new window

# 其他参赛文章

原生预览调试！我给Cocos加了个新功能，原生开发者福音open in new window